应用光学费马原理介绍
定理定律原理 2024-11-08 10:56未知
本文介绍光程的定义和应用,同时详细介绍了费马原理以及如何使用费马原理推导出反射定律和折射定律。这篇文章适合对光学有基础了解的读者阅读。
1.光程
光程是指光在介质中经过的几何路程l与该介质折射率n的乘积,光程用s表示为
由于介质的折射率n是光在真空中的速度c和在介质中的速度ν之比,即
又知光在介质中所经过的路程为
代入式(1)可得
式(2)表明,光在某种介质中的光程等于光在同一时间内在真空中所走过的路程。光程又称为光的“折合路程”。
若光线通过多层(如m层)均匀介质,则光线由许多段折线组成,其光程为
若光线通过连续变化的非均匀介质,即折射率n为位置的函数,则光线实际所走过的路程为一条空间曲线。若光由点A传到点B,则光程可表示为
式中,L为光线在介质中所走过的实际路程。
2.费马原理
费马原理是光线传播规律的另一种表述形式,该原理为:实际光线沿着光程为极值(或稳定值)的路线传播。
费马原理的数学描述:
费马原理又称为“极值光程定律”。满足费马原理时,光程可能为极大值或极小值,可以认为符合费马原理的情况下,光程处于稳定值。
在均匀介质中,根据几何公理“两点间以直线距离为最短”,由费马原理可以直接证明和解释光的直线传播定律。
3.用费马原理推导反射定律
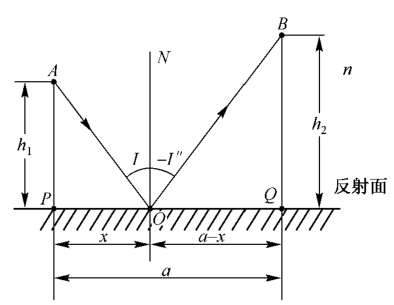
图1:利用费马原理证明反射定律
如图1所示,PQ为平面反射镜,由点A发出的光线投射到反射镜面上的点O,反射后的光线通过点B。设光线处于均匀介质中,折射率为n,投射点O到由点A作反射镜垂线的垂足P的距离为x,则点A到点B的光程长度为
显然,光程s是变量x的函数。
根据费马原理,实际光线的光程是稳定的,在均匀介质中其一阶导数为零,即

从而推导出
即
这就推导出了反射定律。
进而可以证明
这表明满足反射定律的光线具有最短的光程。
4.用费马原理推导折射定律
图2:利用费马原理证明折射定律
如图2所示,由位于折射率为n1的均匀介质中的点A发出光线投射到分界面上的点O,经折射后光线进入折射率为n2的均匀介质,并通过点B。设点O到点A的垂足C点的距离为x,则点A到点B光线的光程可表示为

根据费马原理,实际光线的光程是稳定的,在均匀介质中其一阶导数为零,即
因而有
这就推导出了折射定律。
同样进而可以证明

这表明满足折射定律的光线具有最短的光程。



上一篇:科学之探究:杠杆原理
下一篇:什么是第一性原理?